Concept:
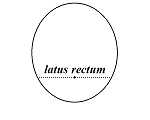
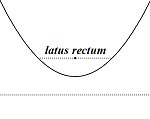
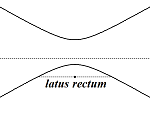
The equations of conic sections in polar form take an especially simple and unified form when a focus is at the pole and an axis is parallel or perpendicular to the ray θ = 0°.
|
|
|
|
Changing the sign in the denominator or changing the trigonometric function used in the denominator to the sine function changes the orientation of the graph, but not its shape or size.