FOCUS ON PROBLEM SOLVING 6

It is often necessary to combine different problem-solving principles. The principles of drawing a diagram and adding something extra are used in Euler's solution of the "Königsberg bridge problem." The problem itself is interesting, but not of great practical importance. However, Euler's solution is so brilliant that it is the basis for a whole field of mathematics called network theory, which has practical applications to electric circuits and economics.

The Königsberg Bridge Problem

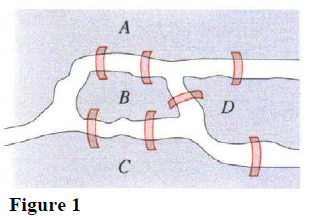
The old city of Königsberg is situated on both banks of the Pregel River and on two islands in the river. Seven bridges connect the parts of the city, as shown in Figure 1. According to local folklore it was impossible to cross all seven bridges in a continuous walk without recrossing any.

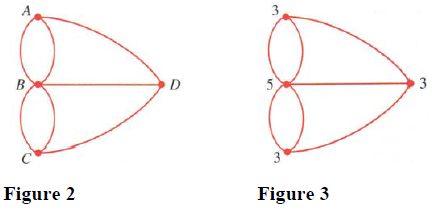
When Euler heard of the problem he realized that an interesting mathematical principle must be at work here. To discover the principle Euler first stripped away the nonessential parts of the problem by drawing a simpler diagram of the city where the land masses are represented by points and the bridges by lines connecting the points (Figure 2). The problem now is to draw the diagram without lifting the pencil and without retracing any lines. To show that this is impossible, Euler added something extra by labeling each point with the number of line segments that end at the point (Figure 3). He then argued that every pass through a point accounts for two line ends (one entering and one leaving). Thus each point, except possibly the starting point and the ending point must be labeled by an even number in order for the walk to be possible. Since there are more than two points labeled by odd numbers, the walk is impossible!

The beauty of Euler's solution is that it is completely general. In modern language a diagram consisting of points and connecting lines is called a network, each point is a vertex, each line an edge, and the number of edges ending at a vertex is the order of the vertex. A network is traversable if it can be drawn in one stroke without retracing any edge. Euler's reasoning about the Königsberg bridge problem shows the following: If a network has more than two vertices with odd order, then it is not traversable.

PROBLEMS

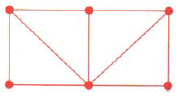
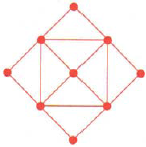
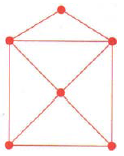
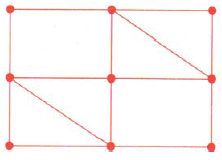
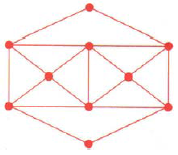
NOTE: Determine if the network is traversable in 1-6. If it is, find a path that traverses it.

1. 
2. 
3. 
4. 
5. 
6. 
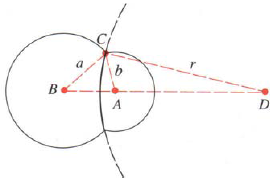
7. When two bubbles cling together in midair, their common surface is part of a sphere whose center $D$ lies on the line passing through the centers of the bubbles. Also, the angles $ACB$ and $ACD$ both have measure 60$^\circ$ (see the figure).
   1. Show that the radius $r$ of the common face is given by $$r = \frac{ab}{a-b}$$
   2. If the radii of the two bubbles are $4$ cm and $3$ cm, respectively, find the radius of the common face.
   3. What shape does the common face take if the two bubbles have radii of the same length?
   
   
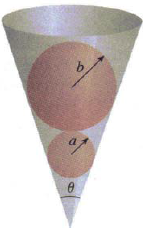
8. A ball of radius $a$ is inside a cone so that the surface of the cone is tangent to the ball. A larger ball of radius $b$ fits inside the cone in such a way that it is tangent to both the ball of radius $a$ and to the sides of the cone. Express $b$ in terms of $a$ and the angle $θ$ shown in the figure.