FOCUS ON PROBLEM SOLVING 12
Many patterns are created in stages. If we can find the rule that leads us from one stage to the next we can then use mathematical induction to prove that the pattern always holds. The following example combines the use of counting principles with mathematical induction to find and prove a surprising formula.
Dividing a Circle into Regions
Choose $n$ different points on the circumference of a circle, then connect the points with line segments in all possible ways. We are interested in the number of regions into which the line segments divide the circle. Let's see what happens for $n =1,2,3,$ and $4$.
With one point on the circle we get one region, with two points two regions, and so on.
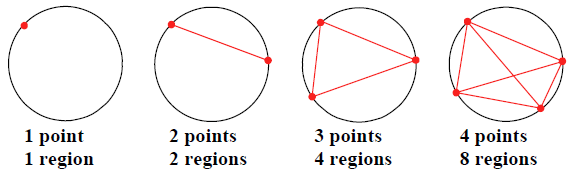
There is a restriction on how we place the points on the circle. The points should be in general position. That is, the points should be placed on the circle in such a way that every intersection point inside the circle is an intersection of exactly two line segments (not more than two).
| Points $n$ | Regions |
|---|---|
| 1 | $1$ |
| 2 | $2$ |
| 3 | $4$ |
| 4 | $8$ |
| 5 | $16$ |
| 6 | $31$ |
The table in the margin gives the number of regions for several values of $n$. It may appear at first that the number of regions is simply powers of two: $1, 2, 4, 8, 16,$ But then for $n = 6$ we get $31$, not the expected $32$. So our initial guess at a pattern is wrong.
It is difficult to count the number of regions directly, so let's try to also count the number of line segments and the number of interior vertices (or intersection points) for a few values of $n$.
| Points $n$ |
Lines $L(n)$ |
Interior Vertices $V(n)$ |
Regions $R(n)$ |
|---|---|---|---|
| 1 | $0$ | $0$ | $1$ |
| 2 | $1$ | $0$ | $2$ |
| 3 | $3$ | $0$ | $4$ |
| 4 | $6$ | $1$ | $8$ |
| 5 | $10$ | $5$ | $16$ |
| 6 | $15$ | $15$ | $31$ |
From the table it appears that for each $n$ we have $$R(n) = L(n) + V(n) + 1$$
Let's use induction to prove this formula.
PROOF BY INDUCTION
Step 1 The formula is clearly true for $n = 1$.
Step 2 Suppose the formula is true for some integer $k$. (This is the induction hypothesis.) Let's consider $k + 1$ points on the circle. Connecting $k$ of these points results in $$R(k) = L(k) + V(k) + 1$$
regions, by the induction hypothesis. Now as we connect the $(k+1)^{st}$ point to each of the other points, observe that every time we cross one of the existing line segments we create a new interior vertex and we divide an old region into two new regions, thus increasing the number of regions by one. But when we reach the endpoint of the segment we divide this final region into two new regions but we do not create a new interior vertex. Thus, for each new line, the number of regions it creates is one more than the number of vertices it creates. So adding a new line segment adds $1$ to $L(n)$, and adds one more to $R(n)$ than it does to $V(n)$, thus preserving the equality in the formula. The figure illustrates this the special case of four points on the circles.

So the equation remains true as we connect the $(k+1)^{st}$ point to each of the old points. That is $$R(k+1) = L(k+1) + V(k+1) + 1$$
This completes the induction step.
FINDING A FORMULA
We have proved an important relationship between the number of points on the circle, the number of interior vertices, and the number of regions. But we have not yet found a formula for the number of regions in terms of $n$, the number of points. To do this we try to find formulas for the numbers $L(n)$ and $V(n)$.
The number of lines $L(n)$ To count the number of lines notice that each pair of points on the circle determines a unique line. So the number of lines is simply the number of ways of choosing two points from the $n$ points on the circle:$$L(n) = C(n, 2)$$
The number of Interior Vertices $V(n)$ To count the number of interior vertices notice that each interior vertex is uniquely determined by $4$ points on the circles (the endpoints of the line segments that intersect at that vertex). So the number of interior vertices is the number of ways of choosing four points from the $n$ points on the circles. So the number of lines is simply the number of ways of choosing two points from the $n$ points on the circle.$$V(n) = C(n, 4)$$
The number of Regions $R(n)$ We can now use the formula relating $R(n)$, $L(n)$, $V(n)$ that we proved above to obtain an explicit formula for $R(n)$. We have $$ \begin{array}{} R(n) &= L(n) + V(n) + 1 &\quad \color{#50F} {Proved \; above} \\ &= C(n, 2) + C(n, 4) + 1 &\quad \color{#50F} {Formulas \; for \; L(n) \; and \; V(n)}\\ &= \frac {n!}{2!(n-2)!} + \frac {n!}{4!(n-4)!} + 1 &\quad \color{#50F} {Formula \; for \; C(n, r)}\\ &= \frac {1}{24}(n^4 - 6n^3 + 23n^2 - 18n + 24) &\quad \color{#50F} {Simplify} \end{array} $$
You can check that this formula yields the correct values for $R(n)$ for the first few values of $n$.
PROBLEMS
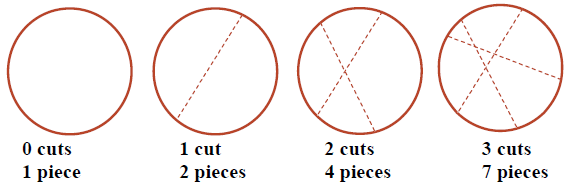
- A pizza is cut by straight cuts, where each cut is made to maximize the number of pieces created. The figure illustrates the situation for $1, 2,$ and $3$ cuts. Find a formula for the number of pieces that result from $n$ such cuts.
- Starting with an equilateral triangle of side $1$, we successively construct new figures with more and more sides as shown. The snowflake curve is the result of repeating this process indefinitely.
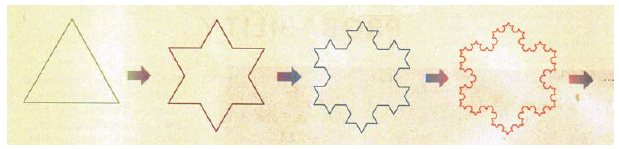
- Find the area enclosed by the snowflake curve. [Hint: This area is the sum of an infinite series.]
- Observe that the length of the snowflake curve is infinite. [Hint: Express the length as an infinite series and show that the series diverges.]
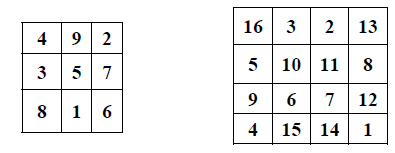
Note: Parts (a) and (b) show that if your lawn has the shape of a snowflake curve, you could easily mow it, because it has finite area, but you could never put a fence along its boundary. - An $n \times n$ magic square consists of the numbers from $1$ to $n^2$ arranged in a square in such a way that the sum of the numbers in a row, column, or diagonal is the same. Let us call this constant sum $S$. Find a formula for $S$ for an $n \times n$ magic square. Here are examples of magic squares
- Consider a $6 \times 6$ grid as shown in the figure.
- Find the number of squares of all sizes in this grid. Generalize your result to an $n \times n$ grid.
- Find the number of rectangles of all sizes in this grid. Generalize your result to an $n \times n$ grid.

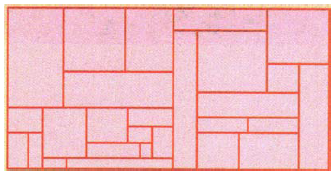
- A rectangle is divided into smaller rectangles in such a way that each of the smaller rectangles has at least one side of integer length. Show that one of the sides of the original, large rectangle must have integer length. [Hint: Imagine the rectangle lying in the coordinate plane, which has been tiled into a checkerboard pattern of black and white squares, each $\frac {1}{2}$ unit by $\frac {1}{2}$ unit. Observe that a rectangle has at least one integer side if and only if its area is composed of equal amounts of black and white.]