FOCUS ON PROBLEM SOLVING 1
One of the most useful tools for problem solving is the principle of recognizing something familiar. In solving a problem several different principles are often involved. In the example we present here we also use the principle of taking cases.
Squares and Primes
Find all natural numbers $n$ such that $n^2 -1$ is a prime number.
SOLUTION
Let's begin by trying a few values for $n$:
| $n$ | $n^2 -1$ |
|---|---|
| $2$ | $3$ |
| $3$ | $8$ |
| $4$ | $15$ |
| $5$ | $24$ |
We see that $n^2 - 1$ is a prime number for $n = 2$, but not for any of the others values of $n$ in this small table. Of course, there may be a very large natural number $n$ for which $n^2 - 1$ is a prime number. No matter how large a table we make, we can't be sure we've found all the values of $n$ for which $n^2 - 1$ is a prime number. So we need to find a more general method.
If we let $p$ represent a prime number, then we are looking for the values of $n$ for which $$p = n^2 - 1$$
We now recognize that the right hand side is a difference of squares. So using the Difference of Squares formula we can write $$p = (n + 1)(n - 1)$$
Since $p$ is a prime number one of the factors on the right-hand side of this equation must be $1$. Let's consider the two cases.
Case I $n + 1 = 1$
In this case we have $n = 0$. But $0$ is not a natural number, so this case is impossible.
Case II $n - 1 = 1$
In this case we have $n = 2$. Then $n^2 - 1 = 2^2 - 1 = 3$ which is a prime number.
We conclude that the only natural number $n$ for which $n^2 - 1$ is a prime number is $2$.
PROBLEMS
- Find all natural numbers $n$ for which $n^3 - 1$ is a prime number.
- Find all prime numbers $p$ for which $2p + 1$ is a perfect square.
- Find all prime numbers $p$ for which $2p + 1$ is a perfect cube.
- Prove that every prime number is the leg of exactly one right triangle with integer sides.
- Show that the equation $$x^2 + y^2 = 4z + 3$$
has no solution in integers. [Hint: Recall that an even number is of the form $2n$ and an odd number is of the form $2n + 1$. Consider all possible cases for $x$ and $y$ even or odd.]
- Prove that it is possible to raise an irrational number to an irrational power and get a rational result. [Hint: The number $a = {\sqrt 2}^{\sqrt 2}$ is either rational or irrational. If $a$ is rational we are done. If $a$ is irrational consider the number $a^{\sqrt 2}$.]
- Use a calculator to evaluate the expressions. You will find that the values are integers. Prove that the calculated values are correct.
- ${\sqrt {3 + 2 \sqrt 2}} - {\sqrt {3 - 2 \sqrt 2}}$
- $\frac{\sqrt 2 + \sqrt 6}{\sqrt 2 + \sqrt 3}$
- An ice cube is floating in a cup of water, full to the brim, as shown in the figure. As the ice melts, what happens? Does the cup overflow, or does the water level drop, or does it remain the same? (You need to know Archimedes' Principle: A floating object displaces a volume of water whose weight equals the weight of the object.)
- A man drives from home to work at a speed of $50$ mi/h. The return trip from work to home is traveled at the more leisurely pace of $30$ mi/h. What is the man's average speed for the round trip?
- A car and a van are parked $120$ mi apart on a straight road. The drivers start driving towards each other at noon at a speed of $40$ mi/h. A fly starts from the front bumper of the van at noon and flies to the front bumper of the car, then immediately back to the front bumper of the van, back to the car, and so on, until the car and the van meet. If the fly flies at a speed of $100$ mi/h, what is the total distance it travels?
- Two runners start running laps at the same time, from the same starting position. George runs a lap in $50$ s; Sue runs a lap in $30$ s. When will the runners next be side by side?
- The ancient Egyptians considered rectangles whose perimeters and areas were numerically the same to be special. Find all rectangles whose perimeter (in feet) and whose area (in ft$^2$) are the same integer.
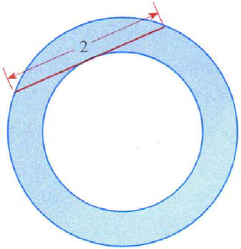
- Find the area of the region between the two concentric circles shown in the figure.
- An extended family consists of the members
{Baby, Son, Daughter, Mother, Father, Uncle, Aunt, Grandma, Grandpa}
listed in increasing order of age. If $x$ and $y$ are members of this family, define $x$ + $y$ to be the older of $x$ and $y$, and define $x \bullet y$ to be the younger of $x$ and $y$.- Find (Baby $+$ Uncle) $+$ Mother.
- Find Father $\bullet$ (Grandpa $+$ Aunt).
- Show that the operations $+$ and $\bullet$ that we have defined satisfy the same Commutative, Associative, and Distributive Properties as do the real numbers with regular addition and multiplication.
- Show that the operations also satisfy the property $$x + ( y \bullet z) = (x + y)\bullet(x + z)$$
Do the operations of regular addition and multiplication with real numbers also satisfy this property?
