DISCOVERY PROJECT

Relations and Functions

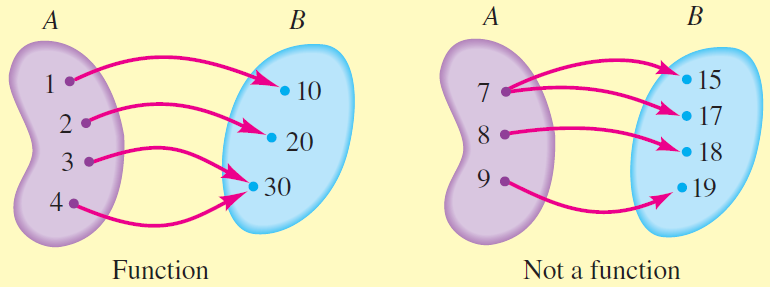
A function $f$ can be represented as a set of ordered pairs $(x, y)$ where $x$ is the input and $y = f(x)$ is the output. For example, the function that squares each natural number can be represented by the ordered pairs $\{(1, 1), (2, 4), (3, 9),...\}$.

A relation is any collection of ordered pairs. If we denote the ordered pairs in a relation by $(x, y)$ then the set of $x$-values (or inputs) is the domain and the set of $y$-values (or outputs) is the range. With this terminology a function is a relation where for each $x$-value there is exactly one $y$-value (or for each input there is exactly one output). The correspondences in the figure below are relations—the first is a function but the second is not because the input $7$ in $A$ corresponds to two different outputs, $15$ and $17$, in $B$.

We can describe a relation by listing all the ordered pairs in the relation or giving the rule of correspondence. Also, since a relation consists of ordered pairs we can sketch its graph. Let's consider the following relations and try to decide which are functions.

(a)   The relation that consists of the ordered pairs $\{(1, 1), (2, 3), (3, 3), (4, 2)\}.$
(b)   The relation that consists of the ordered pairs $\{(1, 2), (1, 3), (2, 4), (3, 2)\}.$
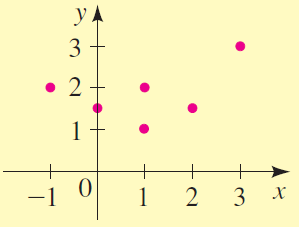
(c)   The relation whose graph is shown to the left.
(d)   The relation whose input values are days in January 2005 and whose output values are the maximum temperature in Los Angeles on that day.
(e)   The relation whose input values are days in January 2005 and whose output values are the persons born in Los Angeles on that day.

The relation in part (a) is a function because each input corresponds to exactly one output. But the relation in part (b) is not, because the input $1$ corresponds to two different outputs $(2$ and $3)$. The relation in part (c) is not a function because the input $1$ corresponds to two different outputs $(1$ and $2)$. The relation in (d) is a function because each day corresponds to exactly one maximum temperature. The relation in (e) is not a function because many persons (not just one) were born in Los Angeles on most days in January 2005.

  1. Let $A = \{1, 2, 3, 4\}$ and $B = \{-1, 0, 1\}$. Is the given relation a function from $A$ to $B$?
    1. $\{(1, 0), (2, -1), (3, 0), (4, 1)\}$
    2. $\{(1, 0), (2, -1), (3, 0), (3, -1), (4, 0)\}$
  2. Determine if the correspondence is a function.
    (a)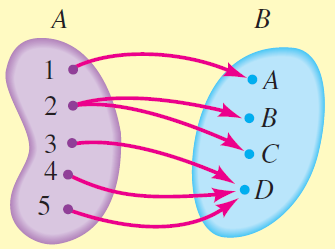
    (b)


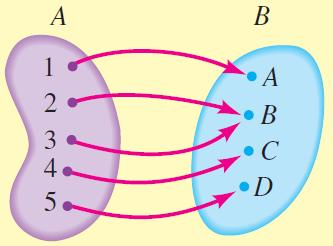
  3. The following data were collected from members of a college precalculus class. Is the set of ordered pairs $(x, y)$ a function?

    (a)
    $x$
    Height    		 $y$
    Weight
    $72$ in. $180$ lb
    $60$ in. $204$ lb
    $60$ in. $120$ lb
    $63$ in. $145$ lb
    $70$ in. $184$ lb
    (b)
    $x$
    Age    		 $y$
    ID Number
    $19$ $82-4090$
    $21$ $80-4133$
    $40$ $66-8295$
    $21$ $64-9110$
    $21$ $20-6666$
    (c)
    $x$
    Year of
    graduation    		 $y$
    Number of
    graduates
    2005 $2$
    2006 $12$
    2007 $18$
    2008 $7$
    2009 $1$

  4. An equation in $x$ and $y$ defines a relation, which may or may not be a function. Decide whether the relation consisting of all ordered pairs of real numbers $(x, y)$ satisfying the given condition is a function.
    (a) $y = x^2$
    (b) $x = y^2$
    (c) $x \le y$
    (d) $2x + 7y = 11$


  5. In everyday life we encounter many relations which may or may not define functions. For example, we match up people with their telephone number(s), baseball players with their batting averages, or married men with their wives. Does this last correspondence define a function? In a society in which each married man has exactly one wife the rule is a function. But the rule is not a function. Which of the following everyday relations are functions?
    1. $x$ is the daughter of $y$ ($x$ and $y$ are women in the United States)
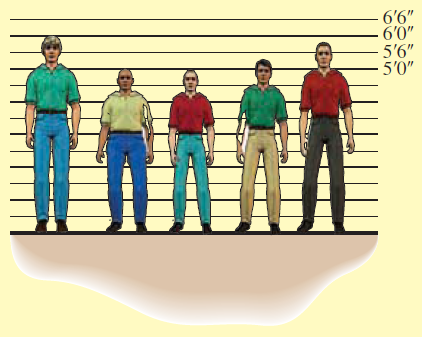
    2. $x$ is taller than $y$ ($x$ and $y$ are people in California)
    3. $x$ has received dental treatment from $y$ ($x$ and $y$ are millionaires in the United States)
    4. $x$ is a digit $(0$ to $9)$ on a telephone dial and $y$ is a corresponding letter