DISCOVERY PROJECT

Sailing Against the Wind

Sailors depend on the wind to propel their boats. But what if the wind is blowing in a direction opposite to that in which they want to travel? Although it is obviously impossible to sail directly against the wind, it is possible to sail at an angle into the wind. Then by tacking, that is, zig-zagging on alternate sides of the wind direction, a sailor can make headway against the wind (see Figure 1).

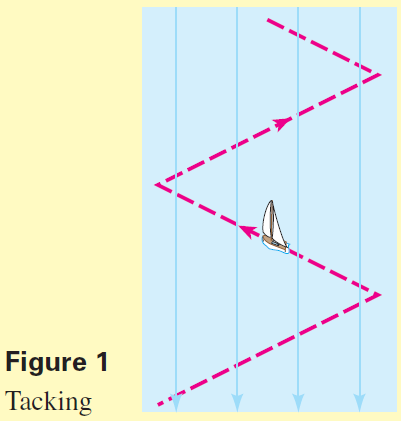
How should the sail be aligned to propel the boat in the desired direction into the wind? This question can be answered by modeling the wind as a vector and studying its components along the keel and the sail.

For example, suppose a sailboat headed due north has its sail inclined in the direction $N \; 20^\circ \; E$. The wind is blowing into the sail in the direction $S \; 45^\circ \; W$ with a force of magnitude $F$ (see Figure 2).

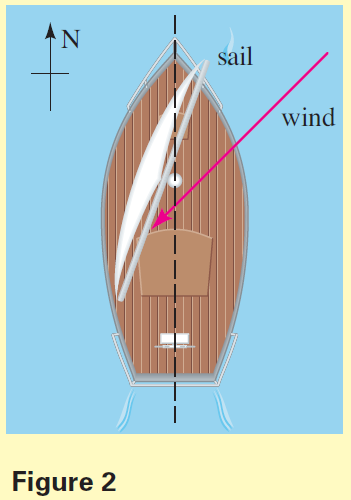
1. Show that the effective force of the wind on the sail is $F$ $\sin 25^\circ$. You can do this by finding the components of the wind parallel to the sail and perpendicular to the sail. The component parallel to the sail slips by and does not propel the boat. Only the perpendicular component pushes against the sail.
2. If the keel of the boat is aligned due north, what fraction of the force $F$ actually drives the boat forward? Only the component of the force found in Problem 1 that is parallel to the keel drives the boat forward.
   

   (In real life, other factors, including the aerodynamic properties of the sail, influence the speed of the sailboat.)

3. If a boat heading due north has its sail inclined in the direction $N \; \alpha^\circ \; E$, and the wind is blowing with force $F$ in the direction $S \; \beta^\circ \; W$ where $0 \lt \alpha \lt \beta \lt 180$, find a formula for the magnitude of the force that actually drives the boat forward.