DISCOVERY PROJECT
Where to Sit at the Movies
Everyone knows that the apparent size of an object depends on its distance from the viewer. The farther away an object, the smaller its apparent size. The apparent size is determined by the angle the object subtends at the eye of the viewer.
If you are looking at a painting hanging on a wall, how far away should you stand to get the maximum view? If the painting is hung above eye level, then the following figures show that the angle subtended at the eye is small if you are too close or too far away. The same situation occurs when choosing where to sit in a movie theatre.

- The screen in a theatre is $22$ ft high and is positioned $10$ ft above the floor, which is flat. The first row of seats is $7$ ft from the screen and the rows are $3$ ft apart. You decide to sit in the row where you get the maximum view, that is, where the angle $θ$ subtended by the screen at your eyes is a maximum. Suppose your eyes are $4$ ft above the floor, as in the figure, and you sit at a distance $x$ from the screen.
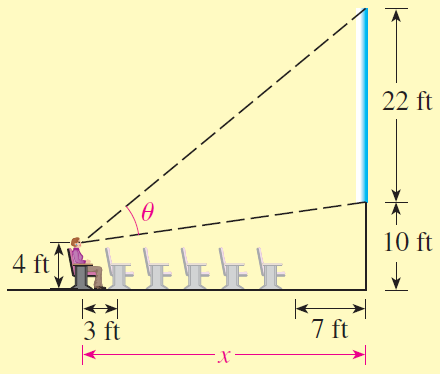
- Show that $θ = \tan^{-1} \left(\frac {28}{x}\right) - \tan^{-1} \left(\frac {6}{x}\right).$
- Use the subtraction formula for tangent to show that $$θ = \tan^{-1} \left(\frac {22x}{x^2 + 168}\right)$$
- Use a graphing device to graph $θ$ as a function of $x$. What value of $x$ maximizes $θ$? In which row should you sit? What is the viewing angle in this row?
- Now suppose that, starting with the first row of seats, the floor of the seating area is inclined at an angle of $\alpha = 25^\circ$ above the horizontal, and the distance that you sit up the incline is $x$, as shown in the figure.
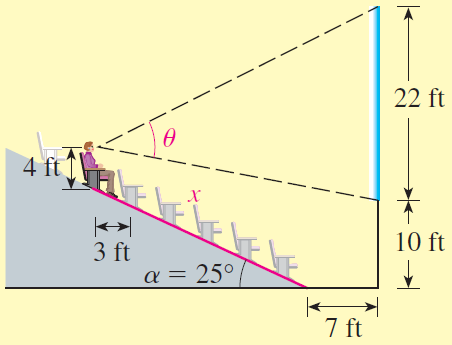
- Use the Law of Cosines to show that
$$θ = \cos^{-1} \left(\frac {a^2 + b^2 -484}{2ab} \right)$$ where $$a^2 = \left(7 + x \; \cos \; \alpha \right)^2 + \left(28 - x \; \sin \; \alpha \right)^2$$ and $$b^2 = \left(7 + x \; \cos \; \alpha \right)^2 + \left(x \; \sin \; \alpha - 6 \right)^2$$ - Use a graphing device to graph $θ$ as a function of $x$, and estimate the value of $x$ that maximizes $θ$. In which row should you sit? What is the viewing angle $θ$ in this row?
- Use the Law of Cosines to show that